weil pairing的双线性特征

点阶与曲线的阶，生成元

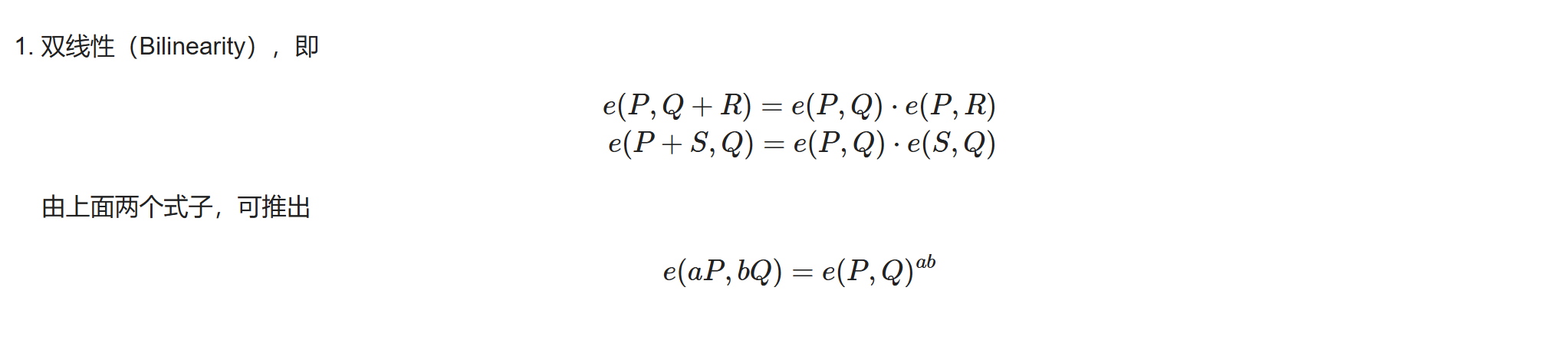
[春秋game冬季赛 day3]dance
题目：

from Crypto.Util.number import *
from secret import flag

m = [int(i) for i in bin(bytes_to_long(flag))[2:].zfill(len(flag) * 8)]

p = 0x1A0111EA397FE69A4B1BA7B6434BACD764774B84F38512BF6730D2A0F6B0F6241EABFFFEB153FFFFB9FEFFFFFFFFAAAB
E = EllipticCurve(GF(p), [0, 4])
G1, G2 = E.gens()
o1, o2 = G1.order(), G2.order()
r = [randint(1, o1 - 1) for _ in range(len(m) + 1)]
c = []
for i in range(len(m)):
    A = r[i] * G1 + m[i] * G2
    B = m[i] * G1 + r[i + 1] * G2
    c.extend(A + B)
open("out.txt", "w").write(f"c = {c}")

解题的诀窍在于 把m两两分为一组，这样有利于找到weil pairing的关系 ，

换言之，可以尝试把线性组合的c与生成元G1或G2进行配对

从上面这个式子看出weil pairing是有序的，

上面这个式子也很重要。

因为是两两一组，所以要么m第一个被落下，要么最后一个。
如果选最后一个被落下的话，只需要知道‘}’的二进制表示的最后一位：1 把它加进去就可以了。

0，1 或 1，0 在筛选出来后我们记后一个数字（即0，1 记为1；1，0 记为0）

exp：

# sage  
from Crypto.Util.number import *  
  
def check(A, B):  
    aa = A.weil_pairing(G1, o1)  
    bb = B.weil_pairing(G2, o2)  
    if aa ^ (-1) == bb:  
        return 0  
    if (aa * e) ^ (-1) == bb:  
        return 1  
    if aa * e ^ (-1) == bb ^ (-1):  
        return 2  
  
c = []   
p = 0x1A0111EA397FE69A4B1BA7B6434BACD764774B84F38512BF6730D2A0F6B0F6241EABFFFEB153FFFFB9FEFFFFFFFFAAAB  
E = EllipticCurve(GF(p), [0, 4])  
G1, G2 = E.gens()  
o1, o2 = G1.order(), G2.order()  
m = []  
C = [E(c[3 * i : 3 * i + 3]) for i in range(len(c) // 3)]  
e = G2.weil_pairing(G1, o1)  
for A, B in zip(C[:-1], C[1:]):  
    u = check(A, B)  
    if u == 0:  
        m.append("x")  
    elif u == 1:  
        m.append(0)  
    elif u == 2:  
        m.append(1)  
    else:  
        print("oops")  
        break  
m += [1]  
while 1:  
    for i, A, B in zip(range(len(m) - 1), C[:-1], C[1:]):  
        u = check(A, B)  
        if u == 0 and m[i + 1] != "x":  
            m[i] = m[i + 1]  
    if "x" not in m:  
        break  
print(long_to_bytes(int("".join(map(str, m)), 2)))

从这道题可以看出来，出题人是精心设计式子，让两两组合在m取0或1时的weil pairing有数量上的关系
这可以称得上是好的出题思路
组合的思路在数学上早已存在很久
同时帮助参赛者更深入了解weil pairing
这给予我灵感 可以出一些体现曲线特征和性质的题：比如说拐点之类的